How to Improve SAT Math Score: What 800 Scorers Actually Do!

Improve SAT Math Score

Most students think improving SAT Math means learning more math — it doesn’t.
The SAT rewards recognition and verification far more than step-by-step solving, which is why capable students still run out of time or make careless mistakes.
Score plateaus usually happen when students prepare harder but not differently.
800 scorers approach the test with a fundamentally different mindset — and that difference is learnable.

I’ve scored a perfect 800 on SAT Math myself, and over the years I’ve helped multiple students reach the same milestone.
But what’s more important is this: I didn’t always think about SAT Math the way I do now.
As I spent more time analyzing real SAT questions and teaching students across score ranges, I realized that the biggest gains didn’t come from learning more math — they came from changing how the test was approached.
The ideas you’ll see here are not theory; they’re the result of what consistently works with real students trying to move from “almost there” to a full score.

Desmos for SAT Math Tips
The shift to the Digital SAT fundamentally changed how SAT Math should be approached, and Desmos is a big reason why.
Desmos isn’t an optional calculator or a shortcut — it’s built directly into Bluebook and is part of how the test is designed to be taken.
Once I started fully leveraging Desmos as a verification and reasoning tool (not just for plotting graphs), my own experience with SAT Math changed completely, and I saw the same shift in my students’ scores.
If you’re not using Desmos — or you’re only using it sparingly — you’re leaving speed, accuracy, and confidence on the table.In today’s SAT, not using Desmos enough is a disadvantage.

The Real Secret Behind an 800 in SAT Math

Every SAT Math question — regardless of topic — can be recognized and approached using a framework.
A framework isn’t a trick or a shortcut; it’s a structured way of identifying what the question is actually testing and choosing the fastest reliable way to deal with it.

800 scorers don’t succeed because they know more math formulas.
They succeed because they’ve practiced enough to instantly place a question into the right framework and execute it with minimal friction.

This is also where many students go wrong with Desmos.
Desmos doesn’t magically save you in the exam hall — it only becomes powerful when you already know what you’re checking. Without frameworks, students either overuse Desmos randomly or avoid it altogether; with frameworks, Desmos becomes a precise verification tool.

One Example Framework: Equivalent Expressions (Using Desmos)

To be clear, SAT Math covers many different skills — algebra, geometry, word problems, statistics, and more.
What follows is just one framework, chosen because it clearly shows how 800 scorers think and how Desmos fits naturally into that thinking.

Questions that ask for equivalent expressions usually make up only a few questions on a test, but they often consume disproportionate time because students try to simplify or manipulate expressions by hand.
An 800-scorer approaches these questions very differently: instead of solving, they check equivalence directly using Desmos.

Equivalent Expressions on the SAT: One Question Type, Three Clear Categories

On the SAT, equivalent expression questions all test the same underlying idea:
you are given one mathematical expression and asked to identify another expression that represents the same function or relationship.

While these questions may look different on the surface—exponents, polynomials, variables, or equations—they can be reliably classified into three types from a solving perspective. Two are multiple-choice, and one is short-answer.

800 scorers don’t treat these as “algebra problems.”
They recognize the type immediately, then apply the fastest correct method—usually with Desmos.

Below are the three types and exactly how they are handled.

Type 1: Single-Variable Expressions (MCQ) → Graph Overlap
In Type 1 questions, you’re given an expression involving a single variable and asked to identify which option is equivalent. Instead of simplifying algebraically, treat the variable as a graphable input in Desmos.
If two expressions are truly equivalent, their graphs will overlap perfectly across the valid domain. Only one answer choice will match exactly.
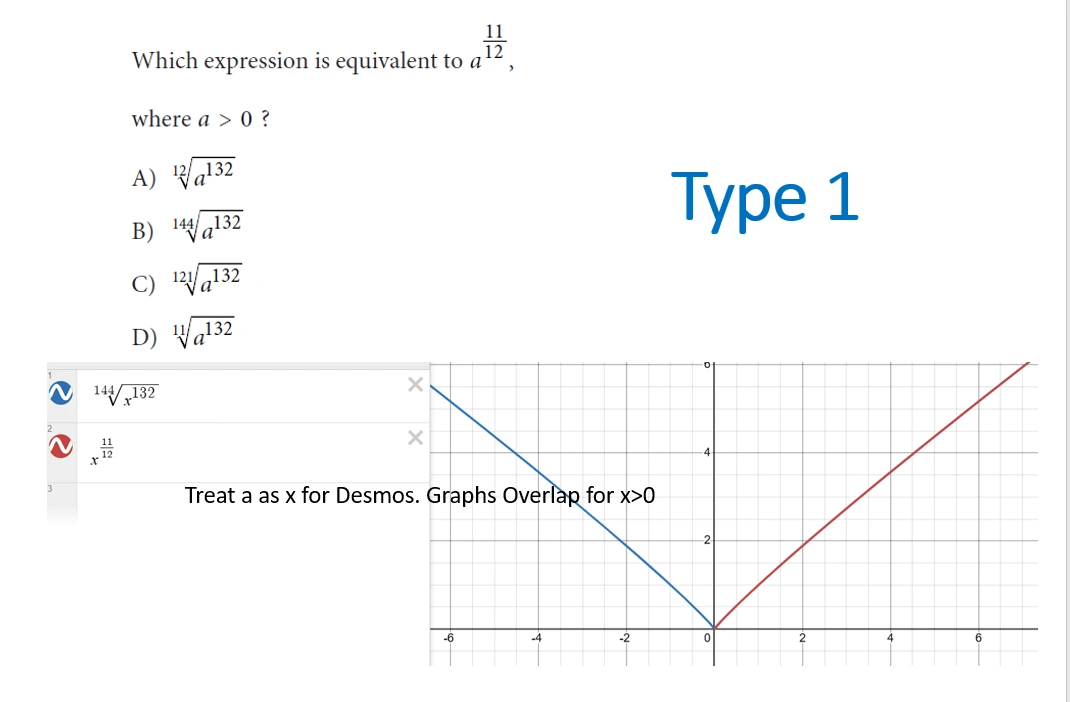
SAT Math equivalent expressions solved using Desmos graph overlap
Type 2: Multiple Variables (MCQ) → Numerical Substitution
When multiple variables are involved, graphing may not be practical. But equivalence still means the expressions must produce the same numerical value for any valid inputs.
Assign simple values to the variables in Desmos, compute the original expression, and check which option matches the result. One correct match is enough.
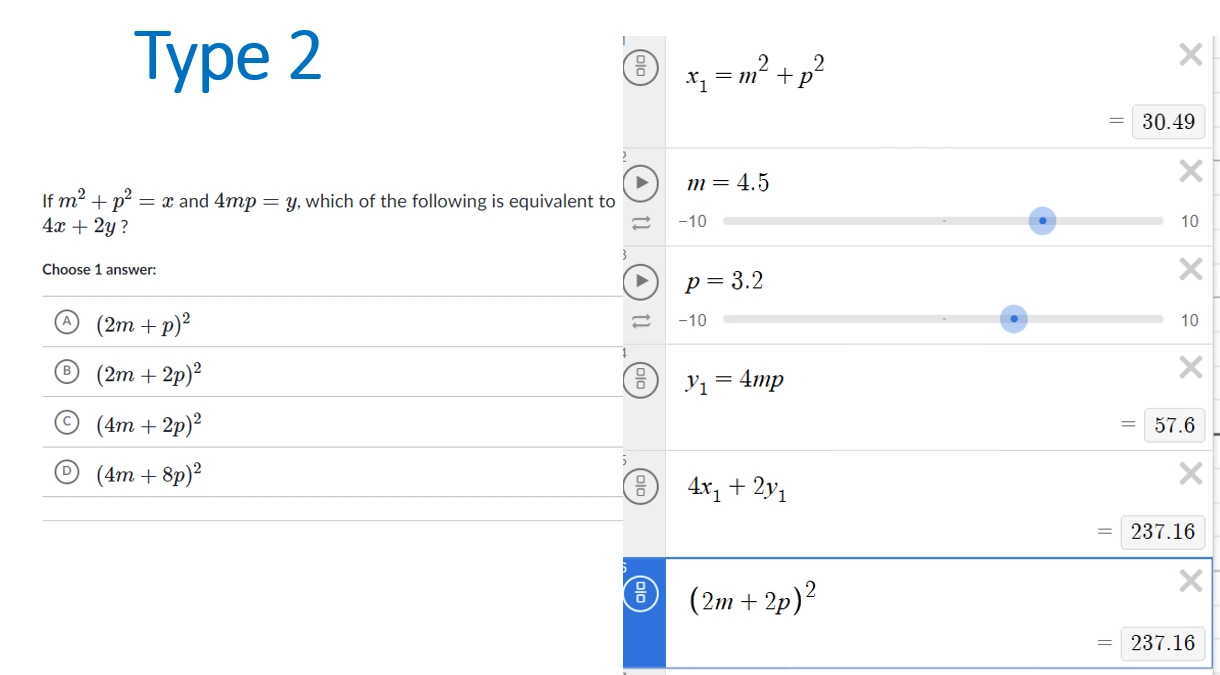
SAT Math multiple variable equivalence checked using Desmos substitution
Type 3: Identity Questions (Short Answer) → True for All Values
These questions look like equations but are not asking you to solve for a variable. Instead, you’re asked to find constants that make both sides identical for all values.
In Desmos, this becomes an identity check. Test multiple values or use regression to determine the constants that enforce equivalence.
SAT Math identity equations verified using Desmos regression
Once you recognize which type you’re dealing with:
  • You don’t hesitate.
  • You don’t debate methods.
  • You don’t rely on hope or intuition.
You apply the right framework immediately — and Desmos becomes a precise tool, not a crutch.
This is exactly how 800 scorers handle these questions.

Book Your Free SAT Trial Class

Start your journey to a 1500+ SAT Score.

Why This Saves Massive Time (and Reduces Mistakes)
Here’s the part most students miss: even deciding how to solve a question costs time.
High scorers don’t deliberate. They don’t pause to ask:
“Should I do this by hand or on Desmos?”
They default to Desmos unless a question is purely interpretive. The decision is already made.
If you save just 30 seconds per question on 20 questions, that’s:
10 minutes saved in a 35-minute module.
That’s the difference between rushing the last few questions and finishing calmly with time to review.
Why This Helps Both Weak and Strong Students
This framework-based approach works across the score spectrum:
  • Struggling students: Fewer steps → fewer arithmetic errors → higher confidence.
  • Mid-to-high scorers (650–750): Less hesitation → better pacing → more consistent scores.
  • Top scorers (750+): Time abundance → fewer careless mistakes → a realistic shot at 790–800.
I’ve seen students move from 400 → 650, and others from 750 → 790/800, using the same underlying philosophy.
A Personal Note
I scored a perfect 800 on SAT Math a couple of years ago. At the time, I didn’t think about the test this way.
Today, after systematizing these frameworks and fully leaning into Desmos , SAT Math feels trivial. I routinely finish Module 2 with 10+ minutes to spare.
Not because I know more math — but because I no longer treat the SAT like a school exam.
Final Thought
Desmos is not the strategy. Frameworks are.
Desmos is simply the fastest way to verify equivalence once you know what you’re looking at.
This is just one framework. SAT Math becomes dramatically easier once you stop solving everything and start classifying and verifying instead.

Related Posts